Teaching Computer Science: Day 12 - It's all about Hex!

In this week’s lesson, I introduced my students to Hexadecimal - explaining why it’s used and how to convert to binary / denary and back again.

Learning Objectives:

• Convert positive denary integers (0‐255) into 2‐digit hexadecimal numbers and vice versa
  
• Convert between binary and hexadecimal equivalents of the same number
  
• Explain the use of hexadecimal numbers to represent binary numbers

Lesson 1: Theory (Hexadecimal)

Suggested time: 50 mins

Starter:

I started by showing two numbers on the board (one in binary and one in hex).

1101 1001
 
C9

I then asked the students, “Which is easiest to remember?”

I explained to students that we often find it difficult to remember long sequences of numbers so, to make life easier, we can break the number down from 4 bits (a nibble) to 1-bit.


Demonstration (Hexadecimal):

Next, I explained that the smallest value we can have in 4-bits (nibble) is 0000 (0 in denary) and the largest value is 1111 (15 in denary) and that we needed to represent each value with a single digit. I then displayed the following table on the whiteboard and asked students to fill in boxes 0-9:

Denary	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15

I then explained that when we reach 10, we hit a problem as we can only use the numerical values 0 – 9.

I then asked the students to suggest ways we would represent the last 6 numbers without using numbers.

I then explained that, to get around this problem, we substitute the numbers 10 to 15 with the letters A to F. I explained that we call this system Hexadecimal (or Hex for short). I followed this by showing the students the following table:

Denary	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Hex	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F

Next, I showed the students, using the following table, what happens when we get to the number 16:

Denary	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31
Hex	10	11	12	13	14	15	16	17	18	19	1A	1B	1C	1D	1E	1F

I explained that when we get to 16, a 1 is added to the front of the next number (highlighting the similarity to the denary system when we go from 9 to 10).

Next, I split the class into groups of three and gave each group a copy of the following table. I then asked them to fill in the blanks:

Denary	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63
Hex

starter.pdf
File Size:	104 kb
File Type:	pdf

Download File

---

I finished by displaying the following table on the board and explained how it could help them in their exam:

Hex	Denary (Decimal)
0F	15
10	16 (1x16)
20	32 (2x16)
30	48 (3x16)
40	64 (4x16)
50	80 (5x16)
60	96 (6x16)
70	112 (7x16)
80	128 (8x16)
90	144 (9x16)
A0	160 (10x16)

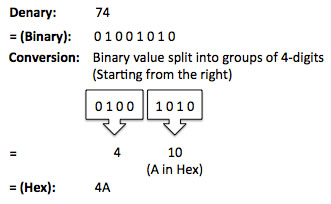
Activity 1 (Denary <--> Hex):

Next I explained that, for the exam, students are expected to be able to convert binary to hexadecimal.

I then showed the students the following video:

I then showed them an example exam question and challenged them solve it:

(a)  Convert the hexadecimal number 6A to denary. (You must show your working out).

.................................................................................................................................

.................................................................................................................................

............................................................................................................................ (2)

I followed this by giving students a series of mini challenges (See answer sheet at bottom of this page):

activity_1.pdf
File Size:	415 kb
File Type:	pdf

Download File

---

Activity 2 (Binary <--> Hex):

Finally I explained that, also for the exam, students are expected to be able to convert binary to hexadecimal.

I explained that, in the exam, students are expected to be able to convert 8-bit binary numbers to hex. I then demonstrated how to do this using the following example:

This was supported by the following help sheet:

bin2hex.pdf
File Size:	108 kb
File Type:	pdf

Download File

---

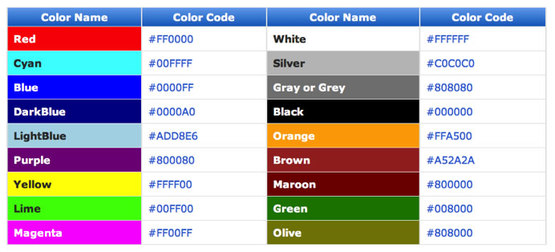
I then showed the students another example exam question and challenged them solve it:

(a)  Convert the binary number 00111101 to hexadecimal.

.................................................................................................................................

.................................................................................................................................

............................................................................................................................ (2)

Plenary:

I finished by putting this all into context. I displayed the following table on the board and asked students if they recognised it. I then asked if they spotted anything familiar (based on the lesson).

I explained that  #FFFFFF = 1111 1111 1111 1111 1111 1111 in Binary which is 16,777,215 in Denary which also happens to be the same number of colours in a web palette! I then asked students to think what it would be like to have to use binary to change the colour of a webpage in HTML!


Homework:

Students were instructed to update their class revision wiki.

Answer Sheets:

Starter:

Denary	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63
Hex	30	31	32	33	34	35	36	37	38	39	3A	3B	3C	3D	3E	3F

Activity 1:

activity_1_answers.pdf
File Size:	418 kb
File Type:	pdf

Download File

---

Useful Links:

How to do Decimal to Hexadecimal Conversion

How to do Binary to Hexadecimal Conversion

---

Lesson 2: Raspberry Pi - Introduction to Python

Suggested time: 50 mins

Main:

Students were instructed to setup their Raspberry Pis and to launch IDLE 3.

Students were then asked to follow Mark Clarckson’s Introduction to Python booklet: (http://community.computingatschool.org.uk/resources/14)


Alternative:

Alternatively, if you do not have access to a set of Raspberry Pis, students can still complete the Python challenges:

To install Python for FREE, go to the python.org website and download a standard installation of the latest version of Python. This will provide you with everything you need.